
The horizontal symmetry of my example loudspeaker assures me that nothing spectacular will occur in the horizontal plane. This will make it easier to see anomalies in the directivity response of the system when the individual sources are combined. To keep things simple, I will model these components as point sources. The second woofer is directly below the first. The horn is located at the top of the baffle. Suppose that you have a two-way loudspeaker system composed of a high-frequency horn and dual 12″ woofers as illustrated in Fig.
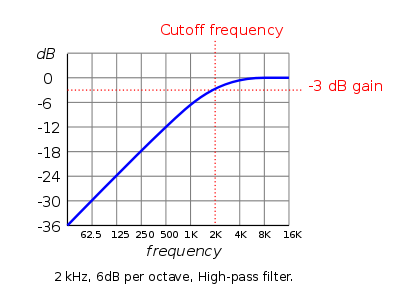
Now that you have a basic understanding of an all-pass filter, let’s put one to good use. The importance of this distinction will become clear later. Low-pass and high-pass filters have only 90° of total phase shift for each order. One difference about all-pass filters is that for each order there is 180° of total phase shift. Low-pass and high-pass filter alignments can also be defined this way. These alignments are not defined by the shape of the magnitude response at the corner frequency of the all-pass-as you typically think of low-pass and high-pass filters-but by the shape of their phase response at the corner frequency. They can be of different orders (i.e., 1st, 2nd, 3rd, and so on) and have specific alignments (Butterworth, Bessel, Linkwitz-Riley, and more). They can be defined mathematically, just as low-pass and high-pass filters can be. There are, of course, other ways to construct all-pass filters. This phase shift is due to the contributions of the low-pass and high-pass filters that were combined (mixed).
There is phase shift associated with this all-pass behavior. Here you see that the magnitude response is perfectly flat it passes all portions of the audio spectrum, thus the name all-pass.

If you were to add the output of these filters back together, essentially combining them with a unity gain mixer, you would get the response in Fig. Figure 2: Magnitude and phase response of the summation of the fourth-order Linkwitz-Riley low-pass and high-pass filters from Fig.


 0 kommentar(er)
0 kommentar(er)
